Flip 3 Coins
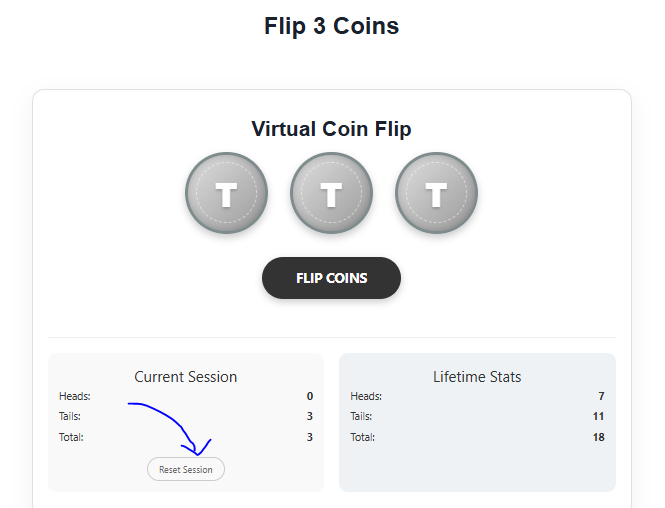
Virtual Coin Flip
Current Session
Lifetime Stats
Flip a Coin three Times
How to Flip a Coin 3 Times
Using our triple coin flip simulator is incredibly simple:
Click the “Flip Coin” Button
All three coins will flip simultaneously with a realistic animation
View Your Results
Check Statistics – Track your personal results and compare with global data
Reset Anytime – Clear your stats and start fresh whenever you want
No registration, no downloads, no hassle. Just pure randomness at your fingertips.
Reasons for 3 Times Coin Flip?
- Decision Making
When you have three people making a choice, or when a simple heads-or-tails isn’t enough complexity, flipping three coins provides eight possible outcomes, giving you more nuanced decision-making power. - Probability Education
Three coin flips perfectly demonstrate fundamental probability concepts. With eight possible outcomes, students can visualize binomial distribution, calculate probabilities, and understand independent events in action. - Group Dispute Resolution
Perfect for groups of three people. Two people can pick heads, one picks tails (or vice versa), and the majority result wins. It’s fairer than just picking one person to decide. - Testing Luck and Patterns
Want to see how rare it is to get all heads or all tails? Flipping three coins multiple times helps you understand statistical probability in a fun, hands-on way. - Game Mechanics
Many games require multiple coin flips to determine outcomes. Our tool eliminates the need for physical coins and speeds up gameplay significantly.
Easy way to understand the Probability of 3 Coin Flips
When you flip three coins, mathematics becomes fascinating. Here’s everything you need to know about the probability behind your tosses.
Total Possible Outcomes: 8
Each coin has 2 possible outcomes (Heads or Tails). When flipping three coins, the total number of possible combinations is:
2³ = 8 possible outcomes
These eight outcomes are:
- HHH – All Heads
- HHT – Two Heads, One Tail
- HTH – Two Heads, One Tail
- HTT – One Head, Two Tails
- THH – Two Heads, One Tail
- THT – One Head, Two Tails
- TTH – One Head, Two Tails
- TTT – All Tails
Each of these eight outcomes has an equal probability of occurring: 1/8 or 12.5%
Probability of Specific Patterns
Getting All the Same (HHH or TTT)
- Probability: 2/8 = 1/4 = 25%
- This means there’s a 1 in 4 chance all three coins land on the same side
- Many people find this surprising because it feels like it should be rarer
Getting Exactly 2 Heads
- Possible outcomes: HHT, HTH, THH
- Probability: 3/8 = 37.5%
- This is the most common pattern with a specific head count
Getting Exactly 1 Head
- Possible outcomes: HTT, THT, TTH
- Probability: 3/8 = 37.5%
- Equally common as getting exactly 2 heads
Getting At Least 1 Head
- Outcomes: All except TTT (7 outcomes)
- Probability: 7/8 = 87.5%
- Very likely to occur!
Getting At Least 2 Heads
- Outcomes: HHH, HHT, HTH, THH (4 outcomes)
- Probability: 4/8 = 1/2 = 50%
- Exactly a coin flip’s chance!
The Binomial Distribution Formula
For those interested in the mathematics, the probability of getting exactly k heads in n flips follows the binomial distribution:
P(X = k) = (n choose k) × (1/2)ⁿ
For 3 flips:
- P(exactly 0 heads) = (3 choose 0) × (1/2)³ = 1 × 1/8 = 12.5%
- P(exactly 1 head) = (3 choose 1) × (1/2)³ = 3 × 1/8 = 37.5%
- P(exactly 2 heads) = (3 choose 2) × (1/2)³ = 3 × 1/8 = 37.5%
- P(exactly 3 heads) = (3 choose 3) × (1/2)³ = 1 × 1/8 = 12.5%
Notice how the probabilities form a pattern: rare at the extremes, common in the middle.
Expected Value
If you flip three coins, on average, you should expect to get 1.5 heads and 1.5 tails (or 3/2 of each). Of course, you can’t actually get half a head, but over many trials, the average converges to this number.
Understanding Independence
This is crucial: each coin flip is completely independent. The first coin’s result doesn’t affect the second or third. Even if you get HH on the first two flips, the third coin still has exactly a 50% chance of being heads or tails.
This independence is why the gambler’s fallacy is a fallacy. If you’ve gotten TTT five times in a row, your next three-flip sequence still has the exact same probability distribution. The coins have no memory.
When to Use the 3 Coin Flip Tool
For Three-Person Groups
- Deciding who pays for lunch among three friends
- Choosing who gets the front seat on a road trip
- Selecting which of three siblings chooses the movie
- Determining turn order in a three-player game
- Picking who does a household chore when there are three roommates
For Multiple Choice Decisions
Assign outcomes to choices:
- HHH: Option A
- HHT, HTH, THH: Option B (3 outcomes = higher probability)
- HTT, THT, TTH: Option C (3 outcomes = equal to Option B)
- TTT: Option D (or re-flip)
Educational Applications
- Teaching probability in math classes
- Demonstrating binomial distribution
- Showing independent events in statistics courses
- Science fair probability experiments
- Homework assignments on combinatorics
- Interactive learning for middle and high school students
Sports and Recreation
- Best-of-three tiebreaker in casual sports
- Determining draft order for fantasy leagues with three participants
- Choosing starting positions in three-way board games
- Settling sports disputes fairly
- Creating mini-tournaments between three players
Daily Life Situations
- Choosing between three restaurants for dinner
- Deciding on weekend activities when there are three options
- Picking which of three movies to watch
- Selecting playlist order for three DJs
- Determining vacation destinations among three choices
Research and Testing
- Monte Carlo simulations requiring random sequences
- Statistical analysis experiments
- Testing randomness generators
- Academic research on probability
- Quality assurance for random algorithms
Real-World Applications of 3 Coin Flips
- Psychology and Decision Science
Researchers use multiple coin flips to study decision-making under uncertainty. Three flips provide enough complexity to test theories about how people perceive and react to random events. - Game Theory
Many strategic games incorporate three-coin flip mechanics to add randomness while maintaining mathematical fairness. The eight possible outcomes create interesting strategic depth. - Computer Science Education
Teaching students about binary numbers and combinations becomes easier with three bits (coin flips). 000, 001, 010, 011, 100, 101, 110, 111 directly correspond to HHH through TTT. - Risk Assessment
Financial analysts sometimes use coin flip scenarios to model binary outcomes in investment scenarios. Three flips can represent a simple three-period model. - Quality Control
Manufacturing processes use random sampling, and three-flip sequences can model pass/fail scenarios across multiple checkpoints.
How Algorithm Works with Fairness in Coin Flip?
True Random Generation
Our three-coin flip simulator uses JavaScript’s cryptographically-enhanced random number generator. Each of the three flips is generated independently with exactly 50% probability for heads or tails.
No Patterns or Biases
Unlike physical coins that might have weight imbalances, wear patterns, or environmental factors affecting them, our digital simulation is purely mathematical. There’s no way to predict the outcome.
Independent Events
Each of the three coins is “flipped” independently. The result of coin 1 doesn’t influence coin 2 or coin 3. This matches the theoretical probability models perfectly.
Verifiable Fairness
Our statistics tracking allows you to verify fairness over time. Flip hundreds or thousands of times, and you’ll see the results converge toward the theoretical probability distribution:
- All same (HHH or TTT): ~25%
- Exactly 1 head: ~37.5%
- Exactly 2 heads: ~37.5%
Comparison with Physical Coins
Physical Triple Coin Flip:
- Difficult to flip three coins simultaneously
- Hard to track which result belongs to which flip
- Environmental factors (wind, surface, hand position) affect results
- Coins can roll off tables or land against objects
- Manufacturing defects might create slight biases
Flipiffy Digital Triple Flip:
- Perfectly consistent 50/50 probability for each coin
- Instant simultaneous results
- Clear display of all three outcomes
- Automatic statistics tracking
- No external factors influence results
- Available anywhere with internet access
Tips for Using the Tool Effectively
For Decision Making
- Assign outcomes clearly before flipping – Decide what each result means before you flip
- Stick with the result – Don’t keep re-flipping until you get what you want
- Use it for neutral decisions – Best when there’s no obviously better choice
- Consider group agreement – Make sure everyone agrees to abide by the result
For Learning Probability
- Make predictions first – Guess what will happen before flipping
- Track results manually – Write down outcomes to see patterns develop
- Flip many times – 30+ flips give better statistical insights
- Compare with theory – Check if your results match expected probabilities
- Test specific scenarios – Try to get HHH five times in a row and see how long it takes
For Games
- Establish rules beforehand – Everyone should know what different outcomes mean
- Use for elimination rounds – Narrow down from many options to few
- Create complexity – Assign point values to different patterns
- Speed up gameplay – Use spacebar for rapid consecutive flips
Common Questions About Flipping 3 Coins
What’s the most common outcome when flipping 3 coins?
Each specific sequence (like HHT) has an equal 12.5% chance. However, getting exactly 2 heads OR exactly 1 head are the most common patterns, each occurring 37.5% of the time.
How rare is it to get all heads (HHH) three times in a row?
Very rare! The probability is (1/8) × (1/8) × (1/8) = 1/512 or about 0.2%. You’d need to flip three coins an average of 512 times to see this happen once.
Can I flip three coins at once in real life?
Yes, but it’s difficult to track which coin is which, and they might roll away or land against something. Our digital tool makes it much easier and more accurate.
Does the order matter in three coin flips?
It depends on your application. In probability calculations, HHT, HTH, and THH are considered different outcomes. But if you only care about the count (2 heads, 1 tail), they’re equivalent.
How many flips until I see all 8 possible outcomes?
This follows the coupon collector problem. On average, you’d need about 22 three-flip sequences to see all eight possible outcomes at least once.
Is your tool really random?
Yes. We use JavaScript’s Math.random() function which provides pseudorandom numbers suitable for non-cryptographic applications. Over large numbers of flips, the distribution matches theoretical probability.
Can I use this for serious decisions?
Our tool provides genuinely random results, but we recommend using comprehensive decision-making for important life choices. It’s great for neutral choices where you’d be happy with any outcome.
Why do I sometimes get the same result many times in a row?
This is normal with random events! Getting HHH five times consecutively has a 1/32,768 chance (about 0.003%), which means it will happen eventually if you flip enough times.
What if I need to flip more than 3 coins?
Check out our other tools! We have options for flipping 2, 4, 5, 10, and even 100 coins at once.
Does the tool work offline?
No, you need an internet connection to access Flipiffy. However, once the page loads, the flipping mechanism works without additional data transfer.
Can I save my flip history?
Your statistics are saved in your browser session. Use the Reset button if you want to clear them and start fresh.
How does this compare to best-of-three single coin flips?
They’re different! Best-of-three means flipping until one side wins twice. That’s a different probability structure than simultaneously flipping three coins once.
The Mathematics Behind Three Flips
Sample Space Visualization
When you flip three coins, imagine a tree diagram:
First Flip: H T
| |
Second Flip: H T H T
| | | |
Third Flip: H T H T H T H T
HHH HHT HTH HTT THH THT TTH TTT
This visual shows all eight equally likely outcomes.
Probability Distribution Table
| Outcome Pattern | Specific Sequences | Count | Probability |
|---|---|---|---|
| 0 Heads (3 Tails) | TTT | 1 | 12.5% |
| 1 Head (2 Tails) | HTT, THT, TTH | 3 | 37.5% |
| 2 Heads (1 Tail) | HHT, HTH, THH | 3 | 37.5% |
| 3 Heads (0 Tails) | HHH | 1 | 12.5% |
Notice the symmetry: 0 and 3 are equally rare, while 1 and 2 are equally common.
Cumulative Probabilities
- At least 1 head: 87.5%
- At least 2 heads: 50%
- At least 3 heads: 12.5%
- At most 1 head: 50%
- At most 2 heads: 87.5%
Conditional Probability Example
If you know the first flip was heads, what’s the probability all three flips are heads?
- Original sample space: 8 outcomes
- Reduced sample space (first flip = H): HHH, HHT, HTH, HTT (4 outcomes)
- Favorable outcome: HHH (1 outcome)
- Probability: 1/4 = 25%
This demonstrates how additional information changes probabilities.
Fun Facts About Triple Coin Flips
The Birthday Problem Connection
Just like the famous birthday paradox, probability with three coins defies intuition. Most people think getting all same (HHH or TTT) is much rarer than its actual 25% probability.
Binary Numbers
The eight outcomes perfectly represent three-bit binary numbers:
- HHH = 111 (7 in decimal)
- HHT = 110 (6)
- HTH = 101 (5)
- HTT = 100 (4)
- THH = 011 (3)
- THT = 010 (2)
- TTH = 001 (1)
- TTT = 000 (0)
Historical Three-Way Decisions
Ancient Romans sometimes used three coin tosses for complex decisions, believing odd numbers had special significance in divination.
The Streak Fallacy
If you flip three coins and get HHH, many people instinctively think the next flip is “due” to include tails. But the probability remains exactly the same: each outcome still has a 12.5% chance.
World Record Attempts
While there are records for consecutive single coin flips landing on the same side (dozens of times), tracking three-coin flip streaks is less common but equally fascinating for probability enthusiasts.
Why People Choose Flipiffy Tool?
- Speed and Efficiency
Get three simultaneous coin flips in under a second. No searching for coins, no fumbling, no drops.
- Perfect for Groups
When three people need to make a decision, everyone can watch the flip happen together in real-time.
Educational Value
Teachers love using our tool for probability lessons. It’s engaging, visual, and demonstrates mathematical concepts clearly.
- Statistics Tracking
Unlike physical coins, we automatically track your results. See how your experimental results compare to theoretical probability. - Universal Access
Works on any device—smartphone, tablet, desktop. No app installation required. - Completely Free
No subscriptions, no ads interrupting your flips, no hidden costs. Just honest, free coin flipping. - Keyboard Controls
Power users can press spacebar for rapid consecutive flips, perfect for probability experiments. - Global Community
Compare your results with millions of other flippers worldwide through our Global Stats feature.
Tips for Teaching Probability with 3 Coin Flips
Classroom Activities
Activity 1: Prediction Challenge Have students predict which outcome will appear most often in 24 flips (3 flips × 8 times). Discuss why exactly 2 heads and exactly 1 head should each appear about 9 times.
Activity 2: Streak Hunt Challenge students to see how many flips it takes to get HHH twice in a row. Discuss why this is rare and calculate the probability (1/64).
Activity 3: Probability Tree Have students draw out the tree diagram showing all eight outcomes, then verify with actual flips from our tool.
Activity 4: Data Collection Assign different students to flip 50 times each, then combine class data to see how 500+ flips converge toward theoretical probabilities.
Activity 5: Simulation vs Reality Have half the class flip physical coins while the other half uses Flipiffy. Compare results and discuss advantages of digital tools.
Learning Objectives Met
- Understanding independent events
- Calculating theoretical probability
- Comparing experimental vs theoretical results
- Recognizing binomial distribution patterns
- Visualizing sample spaces
- Analyzing combinations vs permutations
Advanced: Using Three Coins for More Than Binary Choices
Four-Way Decisions
- HHH: Choice A (12.5% chance)
- HHT, HTH, THH: Choice B (37.5% chance)
- HTT, THT, TTH: Choice C (37.5% chance)
- TTT: Choice D (12.5% chance)
This creates unequal probabilities, which might be useful if you want to weight certain options.
Equal Four-Way Split
Use two outcomes for each choice:
- HHH, HHT: Choice A (25%)
- HTH, HTT: Choice B (25%)
- THH, THT: Choice C (25%)
- TTH, TTT: Choice D (25%)
Tournament Bracket
Use the three flips to seed a tournament between multiple competitors based on their assigned outcome patterns.
Try It Now!
Ready to test your luck with three coins? Click the Flip Coin button above or press spacebar to flip three coins instantly. Watch the animation, see your results, and track your statistics.
Whether you’re settling a three-way debate, teaching probability to students, or just exploring the fascinating world of randomness, Flipiffy’s triple coin flip tool is your perfect companion.
Fair. Fast. Free. Fun.
